Type checking with symbolic execution

U wot m8?

My exploration in the uxn rabbithole continues. Being a stack language, stack juggling is part of the deal. It does get easier with things like keep mode where items are not consumed from the stack but it is still not easy.

To top it off, in uxn, the stack operations can work on either 8-bit or 16-bit numbers: You can push a 16-bit number and pop an 8-bit one out, splitting it in half. The interweb gurus often say: “It will get easier with time”. Maybe it will, but in the mean time, having to step through trivial code with a debugger ¹ just to find simple mistakes is not my idea of a good time.

Being an enjoyer of a high level and highly abstracted language called C ², I told myself there has got to be a better way. uxnbal exists and it has some very good ideas. But I want more.

Having created a language server, I want the errors highlighted right in my editor. The mistakes I made go beyond just stack imbalance: passing arguments in the wrong order, something that happens in other languages too. That means I need a type system.

The goal

• Support the existing notation, verify that a piece of code does in fact have the declared stack effect. The previous link on notation is pretty informative and it will not be replicated here. The syntax is largely derived from Forth. If you are not familiar with stack effect notation, it is recommended to read that before the rest of this post.
• Add a nominal type system. If everything is already a number anyway, just make using numbers a bit safer.
• Try to detect some other errors with load and store:
  • Loading or storing using non-labels due to wrong argument order.
  • Storing to non-data region
• Do not break some common idioms found in existing code base. Some of those will be presented later.

How hard can it be? Turned out: it isn’t. I built it in about a week.

The result (with language server integration) looks like this:

The user-facing documentation can be read here. But this post is about the technical and theoretical part of the implementation. A lot of ideas are lifted straight from https://wiki.xxiivv.com/site/uxntal_notation.html#validation.

Symbolic execution or how I may have misused the term

Wikipedia says ³:

An interpreter follows the program, assuming symbolic values for inputs rather than obtaining actual inputs as normal execution of the program would.

It also says some mumbo jumbo about solving constraints that I didn’t quite get. Another term I’ve found is “abstract interpretation” which is supposedly more general but the material has even more funny symbols and I understood the “symbolic execution” explanation better so let’s stick with that.

In other words: To decide whether a program is correct, execute it. But don’t use actual values, use some sort of abstraction.

So when we see:

@check-this-out ( a b -- )
    POP
    JMP2r

Just execute it and see if it indeed leaves nothing on the stack. Instead of a stack of 256 bytes (or 128 shorts), we define something abstract like:

// Each value is now this struct
typedef struct {
    // In the actual implementation, it's a counted string instead
    const char* name;  
} buxn_chess_value_t;

// A stack is an array of value
typedef struct {
    uint8_t len;
    buxn_chess_value_t content[256];
} buxn_chess_stack_t;

// The VM state is 2 stacks
typedef struct {
    // The working stack
    buxn_chess_stack_t wst;
    // The return stack
    buxn_chess_stack_t rst;
} buxn_chess_state_t;

Seed the buxn_chess_state_t with the initial values:

buxn_chess_state_t state = {
    .wst = {
        .len = 2,
        .content = {
            [0] = { .name = "a" },
            [1] = { .name = "b" },
        },
    },
};

Then run it through the routine. By the time it reaches the return point: JMP2r, we know that the stack now contains a, despite the annotation claiming it to be empty! That’s a stack error right there. Print some pretty error message like:

Output working stack size mismatch: Expecting 0 ( ), got 1 ( a )

The same process can be applied to find out when a stack overflow or underflow happens.

Similarly, nominal type checking is just a matter of:

• Attaching a type label to a value
• When it is passed to a routine, check whether the labels match.

In other words, update the definition to:

// Each value is now this struct
typedef struct {
    // In the actual implementation, it's a counted string instead
    const char* name;  
    // In the actual implementation, it's a counted string and a bit flag
    // But a nullable pointer works too
    const char* type;  
} buxn_chess_value_t;

// We represent a routine signature with this
typedef struct {
    // What the input stacks look like
    buxn_chess_stack_t wst_in;
    buxn_chess_stack_t rst_in;
    // What the output stacks look like
    buxn_chess_stack_t wst_out;
    buxn_chess_stack_t rst_out;
} buxn_chess_signature_t;

Whenever a routine is called, we would check whether the top items of the stacks in buxn_chess_state_t matches what is declared in buxn_chess_signature_t.wst_in and buxn_chess_signature_t.wst_out. The full nominal typing system is explained more here but this is basically the inner working of it: check whether the labels match and print some pretty message if they don’t:

Output working stack #0: A value of type "Card" (Card from card.tal:1:28:27) cannot be constructed from a value of type "Suit" (Suit from card.tal:1:14:13)

uxn has 256 opcodes although they are just variants of 32 base opcodes. The most time consuming part was to implement them again for a “symbolic VM”.

However, there are several problems which are not yet addressed:

• What about branching?
• What about loop?
• What about the size variability unique to uxn (e.g: POP vs POP2)?

They will be addressed in the following sections.

Size variability

The current representation no longer cuts it. Let’s update the value into:

typedef struct {
    // In the actual implementation, it's a counted string instead
    const char* name;  
    // In the actual implementation, it's a counted string and a bit flag
    // But a nullable pointer works too
    const char* type;  
    // In the actual implementation, this is a bit
    bool is_short;
} buxn_chess_value_t;

The stack now becomes:

typedef struct {
    uint8_t len;
    uint8_t size;  //< We will also track size
    buxn_chess_value_t content[256];
} buxn_chess_stack_t;

Whenever a stack item is pushed or popped, the size is also updated along with the length. This means we can quickly detect over or under flow.

All opcodes in uxn are microcoded into PUSH and POP ⁴. ADD is implemented by: POP, POP , add the two numbers and PUSH the result in. The PUSH and POP primitives can now also:

• Split a short value into 2 bytes. For example: #0068 INC will:

  1. Split the short into 00 and 68
  2. POP out the 68
  3. Increment it to 69 ⁵
  4. PUSH it back
  5. We now have: 00 69 as 2 separate items on the symbolic stack.

• Merge 2 bytes into one short. e.g: #01 #02 INC2.

  1. POP2 is run under the hood so merge the 2 bytes into 0102
  2. Increment into 0103
  3. PUSH back
  4. We now have 0103 as a single item on the symbolic stack.

It gets slightly awkward when the sizes are mixed like: #0102 #03 INC2. Here, we would break the first short (0102) and merge it with the lone byte (03).

What about names for pretty error messages? A generation scheme is defined:

• A literal number has its value as the name. e.g: #03 will show up as 0x03 in error messages.
• When a value is modified in-place (i.e: INC), a prime (‘′’) character is appended to its name. e.g: addr* INC2 creates addr′*
• When a short value is split into 2, the 2 halves will the the original name suffixed with -hi and -lo. e.g: short* SWP will create short-lo short-hi.
• When 2 values are combined (e.g: ADD), their names are joined with a dot (·) e.g: a b ADD will create a·b.

Except for the slightly weird names, this works out OK. Moreover, the implementation also tracks the origin of each value (which line and column number created it) so a typical error message looks like:

Input working stack #0: A value of type “Card” (Card from card.tal:4:13:41) cannot be constructed from a value of type “” (0x01 from card.tal:1:7:6)

Preserving nominal type info

Nominal type info can get destroyed by the PUSH and POP micro ops. Suppose that the stack has something like: #01 Apple*, which reads:

• The first item is a literal byte with value: 01.
• The second item is a short which also has the nominal type: Apple.

What happens if we apply ROT to it? ROT has the signature: a b c -- b c a. Intuitively, the stack should now contain: Apple* #01 right? No.

Recall that we implement everything by microcode. ROT is implemented as:

buxn_chess_value_t c = buxn_chess_pop(vm);  // This is polymorphic depending on the opcode flags
buxn_chess_value_t b = buxn_chess_pop(vm);
buxn_chess_value_t a = buxn_chess_pop(vm);

buxn_chess_push(vm, b);
buxn_chess_push(vm, c);
buxn_chess_push(vm, a);

What we get is: Apple-hi Apple-lo #01 instead. When a routine accepting Apple* byte is called, it sees the wrong number of stack items and types. The same would apply to checking the result stack upon return.

But the two halves, Apple-hi Apple-lo, are right next to each other! “Make Us Whole!”, they say. And make them whole we do:

typedef struct {
    // Other members are redacted because they are noise now

    // Once again, a bit field is used in practice
    bool is_lo_half;  // Is this value the lower half?
    bool is_hi_half;  // Is this value the higher half?
    buxn_chess_value_t* whole;  // The original whole value
} buxn_chess_value_t;

Now whenever two halves of the same whole⁶ are next to each other in the correct order, they are merged. To be more precise, this merging happens in the PUSH micro-op. There are also some other details like:

• When a half value is modified in anyway (e.g: ADD, SUB…), it immediately “forgets” about its original whole, preventing merging.
• The whole values are heap allocated, pooled and reused. They are also allocated from an arena so the memory management is fuss free.

With that simple modification, all opcodes are still simply implemented in the canonical microcode definition. The stack can be manipulated in other combinations but whenever the two original halves are next to each other, they retain their original type information.

Branching

Branching presents a bit of a problem. Taking pointers from uxnbal and my understanding of “symbolic execution”, the solution is: just execute all branches.

Whenever a branching opcode is encountered, the symbolic VM state is “forked”. The current execution continues with one of the two branches. The other branch is queued for later. There is already a “verification queue” looking like this:

typedef struct {
    // The routine's name
    const char* name;
    // The signature to check for
    buxn_chess_signature_t signature;
} buxn_chess_routine_t;

typedef struct {
    // The next entry
    buxn_chess_entry_t* next;
    // The corresponding routine
    buxn_chess_routine_t* routine;
    // The initial state
    buxn_chess_state_t state;
    // The starting address in the bytecode
    uint16_t address;
} buxn_chess_entry_t;

For each annotated routines, an entry is created to verify its declared signature. “Forking” is literally just that: Making an exact copy of the current entry but setting a different starting address. Now all branches are accounted for.

Let’s consider this snippet:

@max ( a b -- a-or-b )
    LTHk ?&pick-b ( If a < b, jumps to pick-b )
    POP ( otherwise, pop out b and return )
    JMP2r
&pick-b
    NIP ( remove a and return )
    JMP2r

First, create an entry to verify max:

buxn_chess_routine_t* routine = alloc_routine();
*routine = (buxn_chess_routine_t){
    .name = "max",
    .signature = {
        .wst_in = {
            .len = 2,
            .content = {
                [0] = { .name = "a" },
                [1] = { .name = "b" },
            },
        },
        .wst_out = {
            .len = 1,
            .content = {
                [0] = { .name = "a-or-b" },
            },
        },
    },
};

buxn_chess_entry_t* entry = alloc_entry();
*entry = (buxn_chess_routine_t){
    .routine = routine,
    .state = {
        .wst = {
            .len = 2,
            .content = {
                [0] = { .name = "a" },
                [1] = { .name = "b" },
            },
        },
    },
    .addr = /* address of @max */,
};

enqueue_entry(entry);

When the execution of this entry reached ?&pick-b, we create another entry:

buxn_chess_entry_t* fork = alloc_entry();
*fork = *entry; // Copy state
fork->addr = /* address of max/pick-b */; // Set an alternate address
enqueue_entry(entry); // Enqueue

The existing entry continues to run past the conditional jump.

Loop

Looping presents another problem: a halting one ⁷. I have not read much literatures on this. Based on my reading of uxnbal and some intuition, I came up with a solutions that “seems” correct:

1. Whenever a jump is made from address a to address b, we check whether it has been made before.
2. If this is the first time, mark down that we have made this jump using a hash set of (a, b) pairs, then make the jump.
3. If this is the second time (or later for some reason), stop execution.

The idea is that in case of a loop (backward jump), the loop body is executed at most twice. Let’s assume that the loop will be exited at some point through either:

• A (conditional) jump out somewhere in the middle of the loop (aka a “break””).
• A conditional jump backward (similar to do while (cond) in C).

In both cases, the code after the loop would be entered under two paths:

• One that has executed the loop once.
• One that has executed the loop twice.

If the loop does not have a neutral stack effect (i.e: Making a net growth or shrink in stack size), one of the path will trigger an error upon routine termination. This is because the two paths have different stack sizes, therefore, they cannot both satisfy the same return signature at the same time. Executing the same code just twice should be enough to prove that the stack effect is idempotent ⁸.

To address the previous assumption that “the loop will be exited at some point”, a boolean flag in buxn_chess_routine_t is used to track termination:

typedef {
    // Other fields redacted
    // Whether this routine has terminated
    bool terminated;
} buxn_chess_routine_t;

Whenever an execution has reached a termination point (JMP2r or BRK), this flag is set to true. After all paths have been traced, we check whether this flag is set and emit an error if not.

A general solution to the halting problem does not exist ⁹. But this seems to be a simple approximation that is useful enough for typical loops. It is rather naive and has a few pitfalls.

There may exist a totally unrelated termination path that does not touch the loop. Thus, just because the routine terminates at some point does not mean the code path through the loop does ¹⁰.

Another issue is: as an optimization, whenever an annotated subroutine (e.g: @fn ( b -- c d )) is called, instead of making the jump and continue execution, the signature of the routine is assumed to be correct and applied directly to the stack. For example, suppose that the stack contains a b and a call to fn is made. The stack would be immediately transformed into: a c d without checking the body of fn. This saves a lot of runtime in practice. It is still correct since fn is already queued for verification due to having a declared signature.

However, it assumes that fn also terminates. In the case of mutual recursion (a calls b and b calls a), the assumption might be wrong. I do not yet know how to retain this optimization while still being able to detect obvious unbounded mutal recursion.

Conditional swap

This has been handwaved before but in order to correctly trace execution through jumps, jump addresses must be constants. Typically, they are label references. But literals (e.g: writing out: #0304 literally) can be accepted too although they are strange. Under the hood, “const-ness” is yet another tracked attribute of buxn_chess_value_t:

typedef struct {
    // Other fields...
    bool is_short;  // This was introduced earlier
    bool is_const;  // Whether this is a constant
    uint16_t value;  // The constant value which can also be 8-bit
} buxn_chess_value_t;

A value loses its const-ness when combined with a non-const value (e.g: Through ADD). Any jump following a non-const value is an error because we do not know how to handle it ¹¹. This works well so far until this common idiom in uxntal is encountered:

%max ( a b -- greater ) { LTHk JMP SWP POP }

Let’s trace the stack through each opcode:

a b     ( The initial condition )
a b #01 ( Suppose that a < b, LTHk will push #01 to the stack )
        ( By this point, the pc points at JMP )
a b     ( JMP pops the jump offset from the stack )
        ( The program counter (pc) is now pointing at SWP since it is incremented after fetching an opcode but before its execution )
        ( Because the jump offset is #01, the pc moves ahead and points at POP )
a       ( POP now executes and b is gone )

Let’s look at the other code path where a >= b:

a b     ( The initial condition )
a b #00 ( a >= b )
a b     ( JMP pops the jump offset from the stack )
        ( Because the jump offset is #00, the pc stays at SWP )
b a     ( SWP is executed )
b       ( POP is executed )

It’s a rather clever way of implementing min/max and conditional execution without even using labels. To be able to statically handle this, whenever a boolean opcode is executed, the execution forks. This time, two different values will be pushed into the two paths: 0 and 1 instead of setting two different pc-s.

This seems like a duplicate of branching (conditional jump). However, recall that conditional jump opcodes consume a condition and an address value. The conditional value doesn’t even have to be boolean. The jump is made if the condition is non-zero. Therefore, forking is needed in both cases: One is to handle two possible outputs that can be fed to an unconditional jump. The other is to handle two possible paths of a conditional jump.

If a boolean opcode is followed by a conditional jump (e.g: LTH JCN) which is quite common, the number of paths would explode to 4:

             a b           LTH ( Fork on boolean )
       +------+------+
       |             |
     a b 0         a b 1   JCN ( Fork on conditional jump )
       |             |
    +--+--+       +--+--+
    |     |       |     | 
  jump  noop    jump  noop

There is one set of redudant code paths since effectively, there should be only 2 forks. It is not a problem until one of the “canonical” code paths has some errors and now we are seeing the same message twice.

So maybe don’t fork on constant values? With the presence of loops, it is not so simple. Let’s consider this snippet:

#00

@loop INCk ?loop

POP
BRK

If we do not fork on constant, how would this be traced? Recall that a loop is only run at most twice to check its stack effect. We would get the condition value for ?loop to be #01 and #02 accordingly. Thus, the conditional jump ?loop is taken both times. This would be considered an infite loop while in reality, it will wrap around to 0 and terminates. When in doubt, just mark the special values as being special:

typedef struct {
    // ...
    bool is_fork;  // Whether this value comes from a fork while executing a boolean opcode
} buxn_chess_value_t;

is_fork is another attribute that gets dropped whenever a value is manipulated. Whenever a conditional jump consumes a forked value, it does not fork.

In retrospect, I should have just called it is_boolean. A notation can be given to a boolean value like <name>?. Then, we can have subroutines like: @conditional-op ( a b cond? -- a-or-b ). Passing a non-const boolean to a JMP would not be an error and would just create a fork. For now, such a routine has to be expressed using macro instead.

The lack of a routine boundary

Up until now, “termination” is handwaved. There are 2 types of routine in uxntal:

• Subroutine, is annotated with a dash: ( a b -- c d ). They are usually called using JSR or JSI. A return address would be pushed to the return stack before jumping into the routine. A subroutine terminates with JMP2r: pops an absolute address from the return stack and jumps to it.
• Vector, known elsewhere as “event handler”, is annotated with an arrow: ( a b -> c d ) ¹². A vector terminates with BRK: stopping the current vector execution.

JMP2r cannot be naively considered a termination point because calling an unannotated helper subroutine is a thing:

@public-routine ( a -- )
    helper-routine
    ( do something )
    JMP2r ( public-routine terminates here )

&helper-routine
    ( do something )
    JMP2r ( not here )

Not only that, a vector routine can also call a subroutine as helper.

Fallthrough or tail-call is also common:

@routine-a ( a -- b )
    ( some code )
@routine-b ( a -- b )
    ( some code )
    JMP2r ( this JMP2r is shared )

It is time to realize that: uxntal, unlike many languages, does not have a concept of “function boundary”. It’s a series of instructions that eventually returns or terminates. Consider the classic hello world example:

;text                   ( Push text pointer )

@while                  ( Create while label )

    LDAk DUP ?{         ( Load byte at address, jump if not null )
        POP POP2 BRK }  ( When null, pop text pointer, halt )
    #18 DEO             ( Send byte to Console/write port )
    INC2 !while         ( Incr text pointer, jump to label )

@text                   ( Create text label )
    "Hello 20 "World! 00

The termination point, BRK, is in the middle of the program! Not every vector syntactically ends with BRK. The same can be said for a subroutine: JMP2r can be anywhere. There is no obvious syntactical hints that the routine ends at !while. That’s the reason why all this time, a routine is modelled as a start address instead of a range of address.

Instead of trying to cheat, let’s just properly model call and return. Add another flag to buxn_chess_value_t:

typedef struct {
    // ...
    bool is_return_address;
} buxn_chess_value_t;

Whenever a subroutine is directly queued to verify its signature, a short with is_return_address set to true is pushed to the return stack. Whenever it is jumped to, the current execution trace is considered finished. This is yet another fragile special attribute that will be dropped upon shenanigans.

JMP2r is no longer special under this model. The return address can now be passed around with STHr. It can be split in half and joined whole again. It just can’t be modified. is_return_address represents an “abstract return address” that we do not know the value of. As long as it is jumped to, the routine has “returned”.

All the previous problems disappear. To model call into an unannotated helper routine, just do it:

• Push the return address as usual. This is a constant value since the current pc is known.
• Jump to the routine.

Fallthrough is not special ¹³, just execute until the special return address is jumped to. BRK will terminate the current vector anywhere it is executed.

There is an entire class of bugs that can be caugh by just executing the code:

• Executing into a data region is an error.
• Executing outside of the rom boundary is an error. While memory is initialized to 0 so at runtime, this is probably just BRK, it is an indication of sloppy code.
• Calling BRK from a subroutine is an error.

Working without annotations

All of this work enabling “just execute” as a static analysis method makes annotation optional. The original “Hello world” example can be verified as-is. Without annotation, the address 0x0100 is considered the “reset vector” with the signature ( -> ). This is specified at uxn level.

Annotations are still useful as documentations, nominal typing or for catching errors earlier. Moreover, without assuming Varvara, other vectors can’t be statically discovered without annotations.

But it is now possible for beginners to just start writing uxntal and immediately gets feedback on stack error without learning another new concept.

How did this error happen?

While the assembler can print out a detailed trace of the symbolic execution, sometimes, one just want to know the state of the stack at a certain point. That can be done by writing a special value (2b) to the System/debug port:

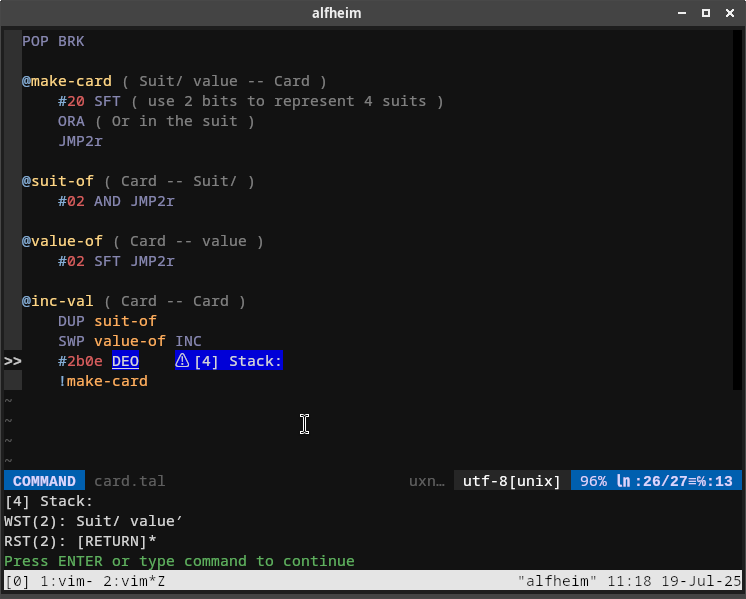
The implementation is straightforward: Every opcode, including DEO already has a handler. Stack printing is just a special case for DEO where the output value and the port are magic constants.

Where to go from here?

Besides addressing existing problems, there are other areas to work on:

• Parallel verification: All verifications are already indpendent, it shouldn’t be hard to paralellize them for a nice speed boost. Currently, this does not seem necessary yet.
• Higher order function: Factor has a nice notation for it: ( a fn: ( a -- b ) -- b ). Supporting this is just a matter of parsing and attaching the type to a buxn_chess_value_t. Indirect jump to values with a function type is no longer an error. The machinery for checking signature and applying stack effect is already there.

Conclusion

The methods presented here are probably not new. But the quirks of uxn do require a few tweaks: Joining half values, jumping on boolean values…

Now that I have a debugger, a type checker and a language server, my experience has been positive so far. I guess the moral of the story is: “If you want to learn how to ride a bike, build the training wheels”.